傳統「九方數多酷」有如分子生物學中的 *資訊完整系統*：如大腸桿菌、黏菌、果蠅、天竺鼠等，此刻正是創新思維、動手開拓的最佳“發展平台”，乃STEAM意念的首段切入口！

今回我給大家示範一個*創意的突破*：

1)  九方共八十一格、填九套字

2)  最少亮字十七個

問：全盤八十一字能構築幾局？

輕輕一問*能砌幾局*是一個耍玩的新命題！它雖不擁抱着傳統遊戲的解題樂趣，卻高舉起*題之不能解*就被靠邊站；所以，明眼人一看就知道「數多酷精粹」之所在，盡在不言中。

那麽，九方中的八十一格設(亮)字佈(單一)局，怎顛來倒去俱可產局，而得出的結果是盈億累萬又是大家熟知的數多酷特色，不在話下。

若用一盤字八十一個字去構築 *兩局* (！)又成嗎？如果您一心以為既然十七個亮字也能構築出十萬個遊戲，四十一個字均勻地散佈開來怎還會出問題呢！？

請看第一圖：Q1是個四十個亮字的標準遊戲題，它的答題是Ans，四十一個藍色數字是原題的配對，你會貿貿然相信一個以藍字為本的Q2是合格標準題嗎？

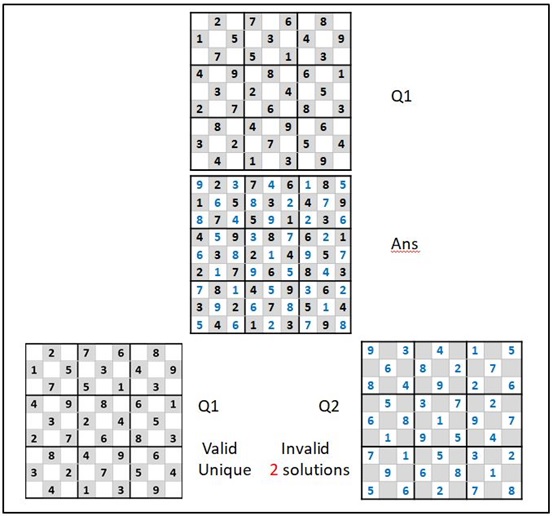
（圖一：Q1是個標準局，它配對出來敞Q2雖有41亮字，卻不能成局！）

如果你這麽相信，就錯了！

把一個四十個亮字的遊戲盤填滿了，天衣無縫，它必然是一個標準「數多酷」遊戲。填進這局的四十一個新字，結果卻不一樣；可以成 (unique) 局，也可以欠一着，或多於一着而“未能成局”。大家不要以為四十一個亮字夠“多”了，看圖二，它甚至多補了卅六個亮字，共七十七個亮字；你仍會發現：最後四格～（哪格該填六、或填八？），還欠邏輯指引，仍不能決定埋尾！因此，這個七十七個亮字的“so called”遊戲，只是個缺失局，並不是唯一（unique）答案的標準數多酷遊戲局。

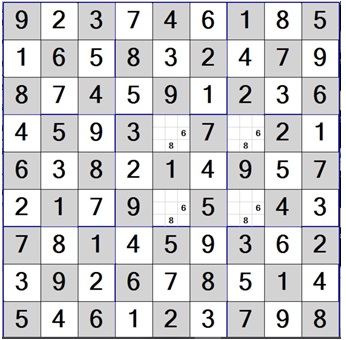
（圖二：雖有41灰底亮字的Q2，多加36個白底數字，卻未能成局！）

有趣的問題可多着：

1)    用上述四十亮字局填好的配對盤、搆築出來的新圖，能產生合標準的遊戲局佔％多少？

2)   除了上述的可能有兩個答案的缺失局外，還有別樣的組合嗎？

3)   既然從初搆時的四十一到最末的七十七亮字都末改缺失構局，不是說明構局時亮字有務虛、無助於解題，那麽，它們對於構築數多酷遊戲到底有啥用？

原圖：作者提供