少時愛玩一個 “填九格” 的遊戲：兩個對手玩，先後輪流在九格盤內劃上 “X” 或 “O” 符號，誰先串連起三格便算贏。 有一回，我構築(設計)了一個不對稱的數多酷遊戲：亮字卅二個，基本上，九宮格內的亮字不是五個就是四個(圖一)，五個如X字、而四個似減格O字。細看第III-V-IIV的三個九宮格剛好連成串(圖二)，贏了！

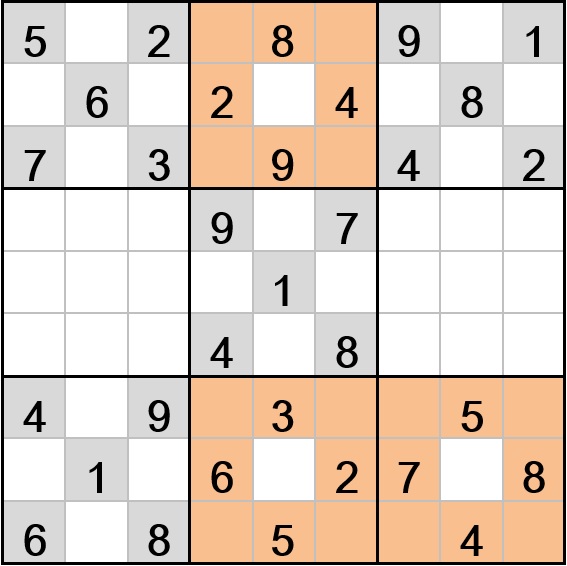
(圖一：X和O的遊戲 )

(圖二：X贏了)

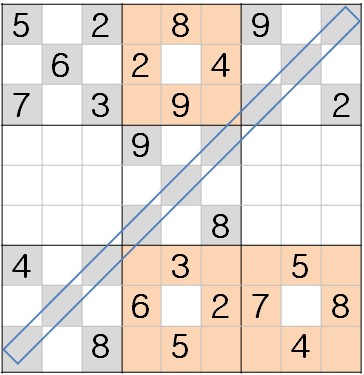
剛好斜線把原來的亮字蔽住，挑起我的懸念：這九個格上的亮字都是缺一不可嗎？ 你來試試！先給你答案(圖三)，我要告訴你：斜。

(圖三：答案)

行能否抽走閒亮字(它的亮字不必顯出)，而原盤的其他字分佈如舊，還成為一局標準的遊戲嗎？(其實，不少遊戲都有閒亮字。閒亮字的存在，一般來說：一來多了閒亮字，局就淺了；二來，閒亮字的分佈往往有助於補救圖形的對稱性，增加美感。) 圖四，紅字是這斜行的三個閒亮字，這局只用廿九亮字便可玩！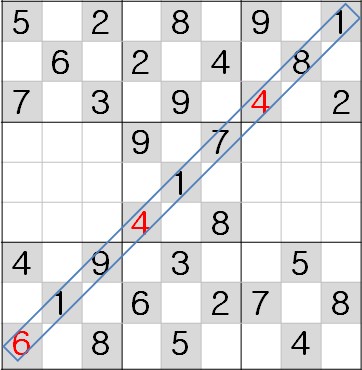

(圖四：三個紅字可以除去)

大家平常玩數多酷不會注意到每一遊戲有沒有閒亮字，倘若我要問大家，有哪種類別的數多酷遊戲，是不假思索、貨真假實，不會出現閒亮字的呢？各位機警的讀者粉絲，您能衝口出個正確答案嗎？ 原圖：作者提供

投票已截止，多謝支持